[LeetCode] 218. The Skyline Problem

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

lefti is the x coordinate of the left edge of the ith building.
righti is the x coordinate of the right edge of the ith building.
heighti is the height of the ith building.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],…]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, […,[2 3],[4 5],[7 5],[11 5],[12 7],…] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: […,[2 3],[4 5],[12 7],…]

Example 1: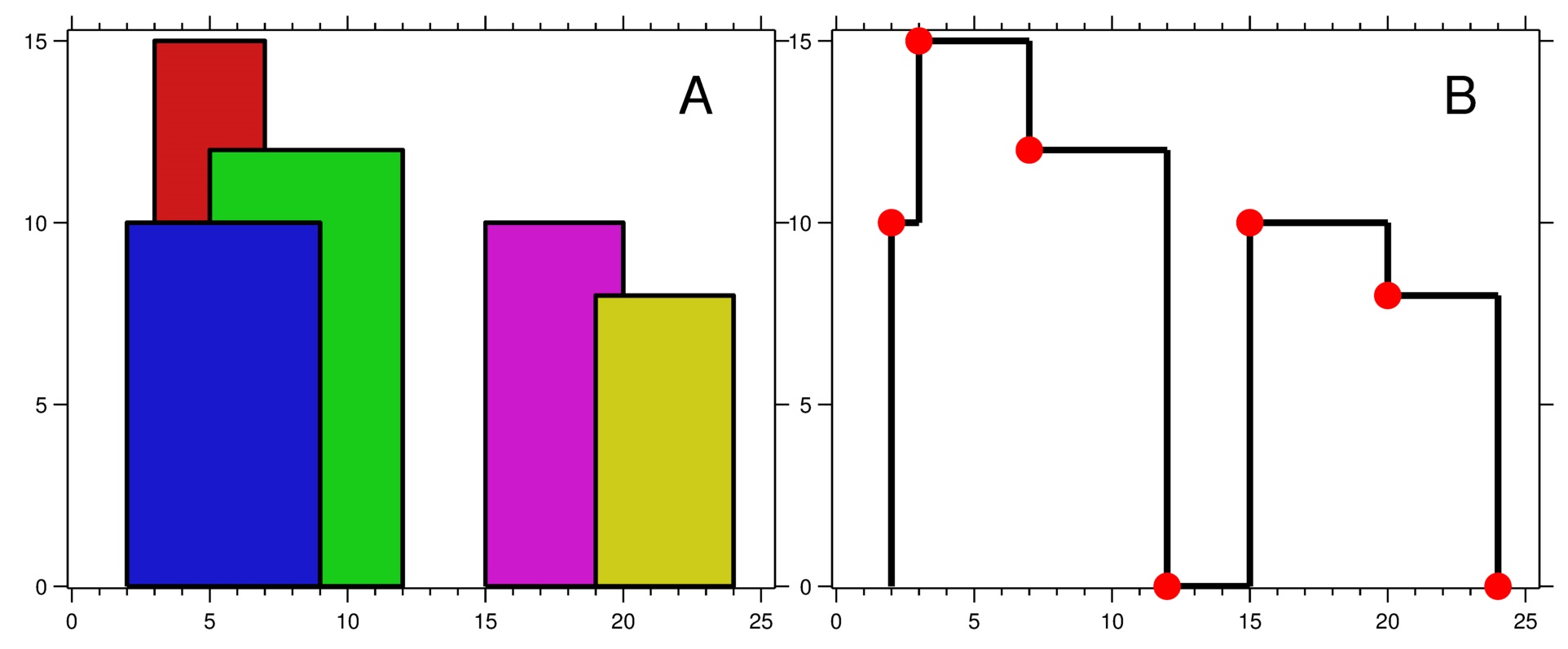

Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:
Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints:
1 <= buildings.length <= 104
0 <= lefti < righti <= 231 - 1
1 <= heighti <= 231 - 1
buildings is sorted by lefti in non-decreasing order.

天际线问题。

城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回 由这些建筑物形成的 天际线 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。
你可以假设所有的建筑都是完美的长方形，在高度为 0 的绝对平坦的表面上。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],…] ，并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[…[2 3], [4 5], [12 7], …]

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/the-skyline-problem
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

题意不难理解，首先，天际线都是一些横的线段，但是最后要求的输出不是线段，而是一些点的坐标。这些点都是一些水平线段的左端点；同时这些点一定是在高度有变化的坐标发生的，但是也分情况，如果高度变大，那么输出的点是高度更大的点；如果高度是变小的，那么输出的点是高度更小的。

思路是扫描线 + 最大堆。因为 input buildings 的形式是 [left, right, height]，表示的是每一个房顶的左边缘，右边缘和高度。我们首先将 input buildings 放入一个 list lines，做一个转换，把每个房子的左边缘和右边缘的高度拆分出来，这样我在 lines 里面存的都是一些边缘和他们各自的高度。但是为了区分左边缘和右边缘，我把左边缘的高度暂时标记成负数。最后我再把 lines 按照高度做一个排序，这样左边缘会相对靠前（都是负数）；如果边缘下标一样，高度更高的靠前。注意这个地方很巧妙地用负数区分了左边缘的高度和右边缘的高度，在排序的时候也确保在遍历左边缘的时候，会先处理高度更高的左边缘，而遇到右边缘的时候，会先处理高度更高的。同时我们需要一个最大堆 maxHeap 和一个变量 preHighest 记录之前最高的高度是多少。

再次遍历 lines，当遇到一个左边缘的时候（< 0），我们把他放到最大堆，但如果是一个右边缘，说明当前这个右边缘所在的矩形处理完了，我们直接从最大堆抛弃这个边。此时如果堆顶元素 curMax 跟之前一个最大高度 preMax 不同的话，堆顶元素 curMax 就是一条天际线的起点，他的下标就是当前遍历到的左边缘的下标。把这个结果加入结果集之后，记得更新 preMax

复杂度

时间O(n^2)
空间O(n)

代码

Java实现

class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        List<List<Integer>> res = new ArrayList<>();
        List<int[]> lines = new ArrayList<>();
        // [left/right, height]
        // 注意矩形左边界的高度被设定为负数了
        for (int[] b : buildings) {
            lines.add(new int[] { b[0], -b[2] });
            lines.add(new int[] { b[1], b[2] });
        }
        
        // 靠左的在前，或者更高的在前
        Collections.sort(lines, (a, b) -> a[0] != b[0] ? a[0] - b[0] : a[1] - b[1]);
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
        maxHeap.offer(0);
        int preHeight = 0;
        for (int[] p : lines) {
            // 左边界 -> 加入高度
            if (p[1] < 0) {
                maxHeap.offer(-p[1]);
            } else {    // 右边界 -> 移除高度
                maxHeap.remove(p[1]);
            }

            int curMax = maxHeap.peek();
            if (curMax != preHeight) {
                res.add(Arrays.asList(p[0], curMax));
                preHeight = curMax;
            }
        }
        return res;
    }
}