[LeetCode] 1615. Maximal Network Rank

There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [ai, bi] indicates that there is a bidirectional road between cities ai and bi.

The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.

The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.

Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.

Example 1: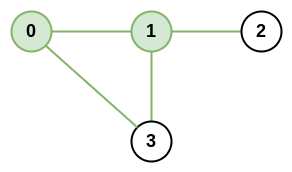

Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.

Example 2: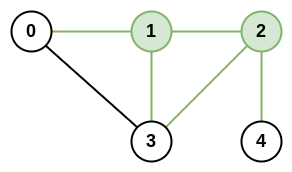

Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
Output: 5
Explanation: There are 5 roads that are connected to cities 1 or 2.

Example 3:
Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
Output: 5
Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.

Constraints:
2 <= n <= 100
0 <= roads.length <= n * (n - 1) / 2
roads[i].length == 2
0 <= ai, bi <= n-1
ai != bi
Each pair of cities has at most one road connecting them.

最大网络秩。

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。

两座不同城市构成的 城市对 的 网络秩 定义为：与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算 一次 。

整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的 最大网络秩 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-network-rank
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

题意如上，本质上是在找 input 里两点之间最大的网络秩 rank。这是一道图论的题，注意每条给出的边都是无向的所以对于一条边上的两个点来说，他们的 rank 都各自 + 1。思路是首先用一个数组 edges 记录每个点各自的 rank 是多少，每遇到一条边，这条边的两端的点的 rank 都各自 + 1；同时我们需要一个二维的邻接矩阵 adj，这里我选择用 boolean，因为我们只需要记录两点之间是否是邻接点即可。

我们遍历一遍 roads 数组之后，我们可以把 edges 数组和 adj 矩阵都统计完毕。之后我们再用两个 for loop 遍历这 n 个点，看看每两个不同的点之间的 rank sum。注意如果两点是能直接相连的，他们在邻接矩阵 adj 里就会是 true，此时 rank 需要减一。

复杂度

时间O(n)
空间O(n)

代码

Java实现

class Solution {
    public int maximalNetworkRank(int n, int[][] roads) {
        // corner case
        if (roads == null || roads.length == 0) {
            return 0;
        }

        // normal case
        int res = 0;
        int rank = 0;
        int[] edges = new int[n + 1];
        boolean[][] adj = new boolean[n][n];
        for (int i = 0; i < roads.length; i++) {
            int from = roads[i][0];
            int to = roads[i][1];
            edges[from]++;
            edges[to]++;
            adj[from][to] = true;
            adj[to][from] = true;
        }

        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                rank = edges[i] + edges[j] - (adj[i][j] == true ? 1 : 0);
                res = Math.max(res, rank);
            }
        }
        return res;
    }
}