[LeetCode] 2684. Maximum Number of Moves in a Grid

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.
Return the maximum number of moves that you can perform.

Example 1: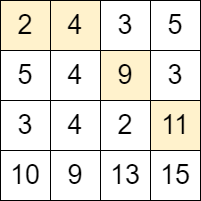

Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
Output: 3
Explanation: We can start at the cell (0, 0) and make the following moves:

• (0, 0) -> (0, 1).
• (0, 1) -> (1, 2).
• (1, 2) -> (2, 3).
  It can be shown that it is the maximum number of moves that can be made.

Example 2: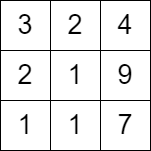

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]
Output: 0
Explanation: Starting from any cell in the first column we cannot perform any moves.

Constraints:
m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 105
1 <= grid[i][j] <= 106

矩阵中移动的最大次数。

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：
从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

思路

题意不难理解，从第一列的任意一个格子出发，看看从左往右最远能走几步。对于某个格子(i, j)来说，他只需要去看这三个格子(i-1, j+1)、(i, j+1)、(i+1, j+1)中的的值是否比自己大，从而决定到底要不要往那个格子走，所以这道题并不是暴力尝试所有的路径。

这里我仍然用 DFS 来做这道题。做的时候，对于(i, j)，如果这三个格子(i-1, j+1)、(i, j+1)、(i+1, j+1)中的的值比(i, j)大，我们才走过去，否则就不要走过去。

复杂度

时间O(mn)
空间O(n)

代码

Java实现

class Solution {
	int count = 0;
	int m;
	int n;

    public int maxMoves(int[][] grid) {
		m = grid.length;
		n = grid[0].length;
		for (int i = 0; i < m; i++) {
			dfs(grid, i, 0);
		}
		return count;
    }

	private void dfs(int[][] grid, int i, int j) {
		count = Math.max(count, j);
		if (count == n - 1) {
			return;
		}
		for (int k = Math.max(i - 1, 0); k <= Math.min(i + 1, m - 1); k++) {
			if (grid[k][j + 1] > grid[i][j]) {
				dfs(grid, k, j + 1);
			}
		}
		grid[i][j] = 0;// backtrack
	}
}