[LeetCode] 304. Range Sum Query 2D - Immutable

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1: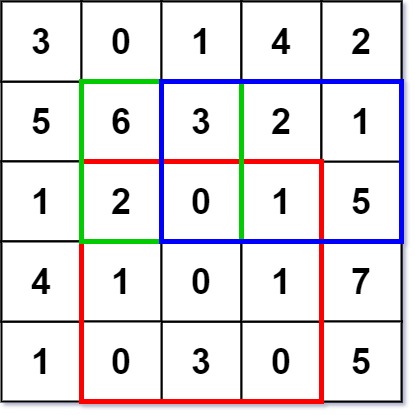

Input
[“NumMatrix”, “sumRegion”, “sumRegion”, “sumRegion”]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-104 <= matrix[i][j] <= 104
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 104 calls will be made to sumRegion.

二维区域和检索 - 矩阵不可变。

给定一个二维矩阵 matrix，以下类型的多个请求：
计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。
实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/range-sum-query-2d-immutable
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

跟303题类似，也是差分数组的题，思路也是前缀和。这里因为 input 矩阵不能修改，我们必须创建一个额外的二维数组记录结果。我这里给一个很好的图示帮助理解。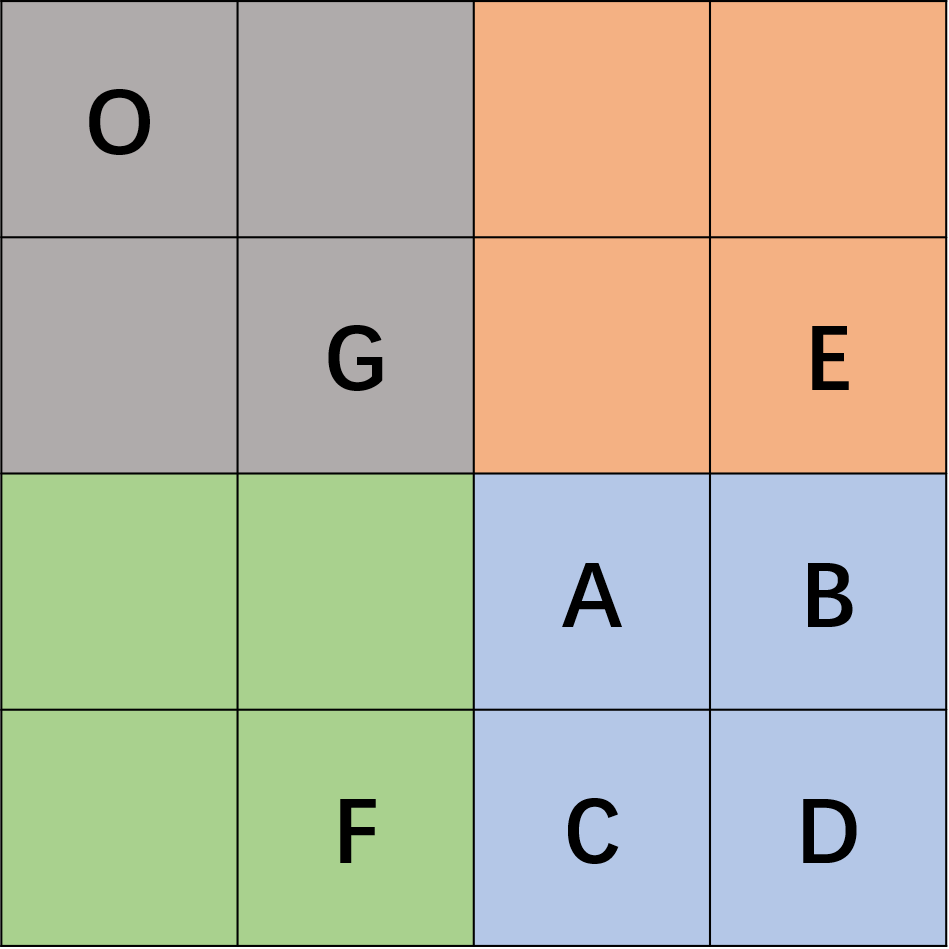

sumRegion(A,D) = sumRegion(O,D) - sumRegion(O,E) - sumRegion(O,F) + sumRegion(O,G)

我们先用一个二维矩阵 grid 记录了整个 input 矩阵的二维前缀和。如果要求整个二维矩阵的前缀和 sumRegion(O, D), 可以直接返回 grid[x + 1][y + 1]，但是上面这个式子记忆的时候下标容易出错，我是这样记的。

OD - OE - OF + OG，中间减去的那两个部分一个需要横坐标 - 1，一个需要纵坐标 - 1

[x2 + 1, y2 + 1] - [x1, y2 + 1] - [x2 + 1. y1] + [x1, y1]

复杂度

时间O(mn)
空间O(mn)

代码

Java实现

class NumMatrix {
	// grid[i+1][j+1] = sumRegion(0,0,i,j)
    int[][] grid;
    
    public NumMatrix(int[][] matrix) {
        // corner case
        if (matrix == null || matrix.length == 0) {
            return;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        grid = new int[m + 1][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                grid[i + 1][j + 1] = grid[i + 1][j] + grid[i][j + 1] + matrix[i][j] - grid[i][j];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
		// [x2 + 1, y2 + 1] - [x1, y2 + 1] - [x2 + 1, y1] + [x1, y1]
		// [22, 12, 21, 11]
        return grid[row2 + 1][col2 + 1] - grid[row1][col2 + 1] - grid[row2 + 1][col1] + grid[row1][col1];
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

[LeetCode] 304. Range Sum Query 2D - Immutable

思路

复杂度

代码

相关题目