[LeetCode] 1457. Pseudo-Palindromic Paths in a Binary Tree

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1: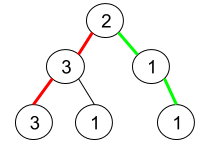

Input: root = [2,3,1,3,1,null,1]
Output: 2
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2: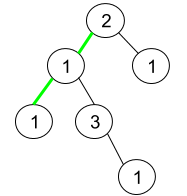

Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:
Input: root = [9]
Output: 1

Constraints:
The number of nodes in the tree is in the range [1, 105].
1 <= Node.val <= 9

二叉树中的伪回文路径。

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

思路

前序遍历 + 回溯。用前序遍历的方法遍历整棵树，在遍历的过程中记录用一个长度为 10 的数组记录每个不同 node.val 的出现次数。遍历到叶子节点的时候看一下数组里出现次数为奇数的元素有几个，如果有超过1个元素的出现次数为奇数，那么当前这条从根节点到叶子节点的路径就不是回文路径。

复杂度

时间O(n)
空间O(n)

代码

Java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
	int count = 0;

	public int pseudoPalindromicPaths(TreeNode root) {
		int[] map = new int[10];
		helper(root, map);
		return count;
	}

	private void helper(TreeNode root, int[] map) {
		// base case
		if (root == null) {
			return;
		}
		map[root.val]++;
		if (root.left == null && root.right == null) {
			if (isPalindrome(map)) {
				count++;
			}
		}
		helper(root.left, map);
		helper(root.right, map);
		map[root.val]--;
	}

	private boolean isPalindrome(int[] map) {
		int single = 0;
		for (int i = 0; i < map.length; i++) {
			if (map[i] % 2 == 1) {
				single++;
			}
		}
		return single > 1 ? false : true;
	}
}