[LeetCode] 785. Is Graph Bipartite

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u).

There are no parallel edges (graph[u] does not contain duplicate values).

If v is in graph[u], then u is in graph[v] (the graph is undirected).

The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1: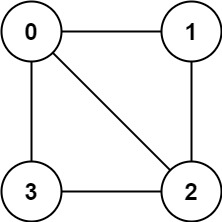

Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.

判断二分图。

存在一个无向图，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：不存在自环（graph[u] 不包含 u）。不存在平行边（graph[u] 不包含重复值）。如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。二分图定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为二分图。
如果图是二分图，返回 true ；否则，返回 false 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/is-graph-bipartite
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

思路是涂色法，只是涂色的方式不同。涂色法大致的思路是，当你遍历 graph 里面的节点的时候，当遇到某一个节点，如果他没有被染色，你就试图给他染成某一种颜色，但是对于这个点的所有邻居节点，需要给他们染成一个别的颜色以区分开。照着这个思路，你需要确保邻居节点被染成不同的颜色。如果遍历结束，所有节点都被染色成功，则说明是一个二分图；如果在染色过程中发现有节点已经被染色但是染色错误，则这个图不是二分图。这里我提供 BFS 和 DFS 两种实现。

复杂度

时间O(V+E) - V是节点数，E是边数
空间O(n)

代码

BFS实现

class Solution {
    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        int[] color = new int[n];
        for (int i = 0; i < n; i++) {
            if (graph[i].length != 0 && color[i] == 0) {
                color[i] = 1;
                Queue<Integer> queue = new LinkedList<>();
                queue.offer(i);
                while (!queue.isEmpty()) {
                    int cur = queue.poll();
                    for (int nei : graph[cur]) {
                        if (color[nei] == 0) {
                            color[nei] = color[cur] == 1 ? -1 : 1;
                            queue.offer(nei);
                        } else if (color[nei] == color[cur]) {
                            return false;
                        }
                    }
                }
            }
        }
        return true;
    }
}

DFS实现

class Solution {
    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        int[] colors = new int[n];
        for (int i = 0; i < n; i++) {
            if (colors[i] == 0 && !dfs(graph, colors, i, 1)) {
                return false;
            }
        }
        return true;
    }

    private boolean dfs(int[][] graph, int[] colors, int node, int color) {
        colors[node] = color;
        for (int nei : graph[node]) {
            if (colors[nei] == 0) {
                if (!dfs(graph, colors, nei, -color)) {
                    return false;
                }
            } else if (colors[nei] == color) {
                return false;
            }
        }
        return true;
    }
}

[LeetCode] 785. Is Graph Bipartite

思路

复杂度

代码

BFS实现

DFS实现

相关题目