[LeetCode] 2116. Check if a Parentheses String Can Be Valid

A parentheses string is a non-empty string consisting only of ‘(‘ and ‘)’. It is valid if any of the following conditions is true:
It is ().
It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
It can be written as (A), where A is a valid parentheses string.
You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of ‘0’s and ‘1’s. For each index i of locked,

If locked[i] is ‘1’, you cannot change s[i].
But if locked[i] is ‘0’, you can change s[i] to either ‘(‘ or ‘)’.
Return true if you can make s a valid parentheses string. Otherwise, return false.

Example 1: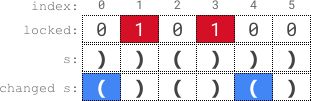

Input: s = “))()))”, locked = “010100”
Output: true
Explanation: locked[1] == ‘1’ and locked[3] == ‘1’, so we cannot change s[1] or s[3].
We change s[0] and s[4] to ‘(‘ while leaving s[2] and s[5] unchanged to make s valid.

Example 2:
Input: s = “()()”, locked = “0000”
Output: true
Explanation: We do not need to make any changes because s is already valid.

Example 3:
Input: s = “)”, locked = “0”
Output: false
Explanation: locked permits us to change s[0].
Changing s[0] to either ‘(‘ or ‘)’ will not make s valid.

Constraints:
n == s.length == locked.length
1 <= n <= 105
s[i] is either ‘(‘ or ‘)’.
locked[i] is either ‘0’ or ‘1’.

判断一个括号字符串是否有效。

一个括号字符串是只由 '(' 和 ')' 组成的 非空 字符串。如果一个字符串满足下面 任意 一个条件，那么它就是有效的：

字符串为 ().
它可以表示为 AB（A 与 B 连接），其中A 和 B 都是有效括号字符串。
它可以表示为 (A) ，其中 A 是一个有效括号字符串。
给你一个括号字符串 s 和一个字符串 locked ，两者长度都为 n 。locked 是一个二进制字符串，只包含 ‘0’ 和 ‘1’ 。对于 locked 中 每一个 下标 i ：

如果 locked[i] 是 ‘1’ ，你 不能 改变 s[i] 。
如果 locked[i] 是 ‘0’ ，你 可以 将 s[i] 变为 ‘(‘ 或者 ‘)’ 。
如果你可以将 s 变为有效括号字符串，请你返回 true ，否则返回 false 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/check-if-a-parentheses-string-can-be-valid
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

遇到括号配对的题，大概率会涉及到 stack，以及需要从左往右 + 从右往左扫两遍。这么做的目的是抓到多余的左括号和多余的右括号。这道题的思路也很接近，不过这道题多给了一个数组 locked，表示可以改动的括号的方向。我们的做法依然还是扫两遍，第一遍我们从左往右扫描，扫描的时候我们用一个变量 count 统计左括号和可以改动的括号（locked.charAt(i) == 0）的数量，这样当我们遇到右括号的时候，我们可以把左括号抵消。当左括号被抵消完毕之后，我们可以再用那些可以改动的括号来抵消更多的右括号，直到那些可以改动的括号被用完为止。

第二遍从右往左扫描的时候，我们用变量 count 统计右括号和可以改动的括号（locked.charAt(i) == 0）的数量，这样当我们遇到左括号的时候，我们可以把右括号抵消。思路跟第一遍一样只是括号方向相反。

最后还有一个例外情况是如果统计到的半括号 + 可以改动的半括号的数量是奇数，就说明括号是无法成对的，就返回 false。

复杂度

时间O(n)
空间O(n)

代码

Java实现

class Solution {
    public boolean canBeValid(String s, String locked) {
        char[] words = s.toCharArray();
        char[] lock = locked.toCharArray();
        int n = s.length();
        int count = 0;
        for (int i = 0; i < n; i++) {
			// 遇到左括号或者当前位置是可以修改的，则count++
			// 如果当前位置是右括号，则count--
            if (words[i] == '(' || lock[i] == '0') {
                count++;
            } else if (words[i] == ')') {
                count--;
            }
            if (count < 0) {
                return false;
            }
        }
        if (count % 2 == 1) {
            return false;
        }

        count = 0;
        for (int i = n - 1; i >= 0; i--) {
			// 遇到右括号或者当前位置是可以修改的，则count++
			// 如果当前位置是左括号，则count--
            if (words[i] == ')' || lock[i] == '0') {
                count++;
            } else if (words[i] == '(') {
                count--;
            }
            if (count < 0) {
                return false;
            }
        }
        if (count % 2 == 1) {
            return false;
        }
        return true;
    }
}