[LeetCode] 951. Flip Equivalent Binary Trees

For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.

Example 1: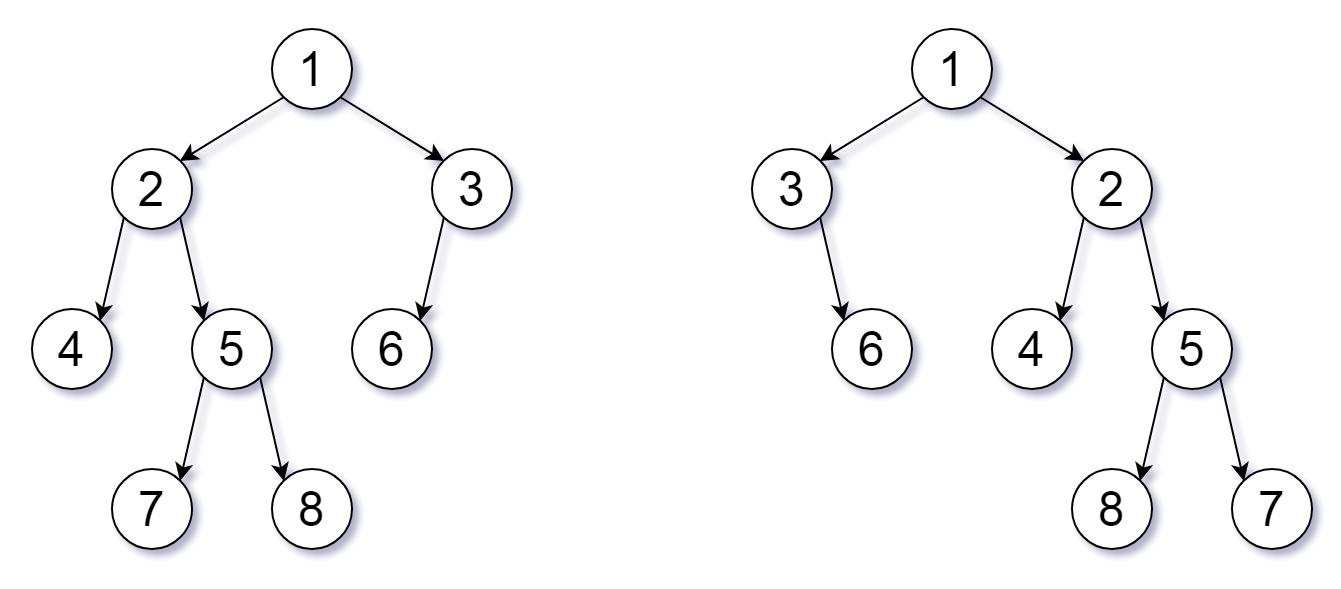

Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.

Example 2:
Input: root1 = [], root2 = []
Output: true

Example 3:
Input: root1 = [], root2 = [1]
Output: false

Constraints:
The number of nodes in each tree is in the range [0, 100].
Each tree will have unique node values in the range [0, 99].

翻转等价二叉树。

我们可以为二叉树 T 定义一个 翻转操作 ，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y，我们就称二叉树 X 翻转 等价 于二叉树 Y。

这些树由根节点 root1 和 root2 给出。如果两个二叉树是否是翻转 等价 的函数，则返回 true ，否则返回 false 。

思路

题意很直观，判断两棵树是否能通过翻转操作变成一样的。那么大致思路就是从根节点往下看，如果 root 节点一样，就往下看；下一层如果左节点 == 左节点，右节点 == 右节点或者 A 的左节点 == B 的右节点，则说明二者可以通过翻转操作变成一样的。用 DFS 的方法遍历整棵树。

复杂度

时间O(n)
空间O(h) - 树的高度

代码

Java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public boolean flipEquiv(TreeNode root1, TreeNode root2) {
        if (root1 == root2) {
            return true;
        }
        if (root1 == null || root2 == null || root1.val != root2.val) {
            return false;
        }
        return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right))
                || (flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left));
    }
}